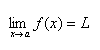2.4: The Precise Definition of a Limit
Hello class.
Lately we've been defining limits in a vague way. Now, with Mr. French's help, we've learned to be more precise in our definitions. I will attempt to review the notes for 2.4 forthwith.
The Book's "precise definition" of a limit is as follows:
"Let f be a function defined on some open interval that contains the number a, except possibly at a itself. Then we say that the limit of f(x) as x approaches a is L, and we write
lim (x-->a) f(x) = L
if for every number e (epsilon) > 0 there is a number d (delta) > 0 such that
|f(x) - L| < e whenever 0 < |x-a| < style="font-style: italic;">a because a is sometimes discontinuous.
By making an interval around the x value, also called d, we may find the corresponding interval around the y value, or e. Sometimes, if we are finding, say, the d interval using the e interval, it will not be evenly distributed about the x value. In this case, we must choose the lesser distance, because that is the distance that does not surpass the interval in either direction on the x-axis.
When using one-sided limits, we restrict the interval to lie on one side of the x interval, left or right for left and right hand limits, respectively.
For example, let's take y = e ^ x.
Now, we know that y = e ^ x is an exponential function, and therefore has a constantly changing slope. Thus, we can assume that the interval we are finding is also uneven. Here is the problem.
Given lim (x-->2) e^x, find delta if epsilon equals .05
Since epsilon is our interval around y, or e ^ 2, we know that our interval ranges from (e ^ 2) + .05 to (e ^ 2) - .05. So, to find our x interval, we must first find the x values that correspond to our y values. The simplest way to do this is to graph y = e ^ x, y= (e ^ 2) + .05, and y= (e ^ 2) - .05, and find where the curve intersects with both lines. We can also use logs to solve this algebraically, plugging (e ^ 2) + .05 and (e ^ 2) - .05 into the y value of y = e ^ x and solving for x. Either way, we get our corresponding x values to be 1.993 and 2.006.
Now we must consider the distances from the ends of our x interval, which ranges from 1.993 to 2.006, to 2, our original x value. With some nifty subtraction, we come up with .007 and .006. Therefore our delta value is .006, as .007 would pass the x interval on the right side, whereas .006 stay within our limits.
There you go. I feel so much more precise. How about you? Don't worry. If you don't, here is a link to another website to make you feel better. It always makes me happy when I'm feelin' blue.
The Precise Definition of a Limit
A Reminder. John, you're posting next.
Here's part of a poem by Emily Dickenson that I like that has the number one in it, a number widely accepted in most states.
To make a prairie it takes a clover and one bee,
One clover, and a bee,
And revery.
The revery alone will do
If bees are few.
To lose one's faith surpasses
The loss of an estate,
Because estates can be
Replenished, faith cannot.
Inherited with life,
Belief but once can be;
Annihilate a single clause,
And Being 's beggary.
Afraid? Of whom am I afraid?
Not death; for who is he?
The porter of my father's lodge
As much abasheth me.
Of life? T'were odd I fear a thing
That comprehendeth me
In one or more existences
At Deity's decree.
Of resurrection? Is the east
Afraid to trust the morn
With her fastidious forehead?
As soon impeach my crown!
Have a nice day, class.