Section 2.2 and such

Hello, this is Evan, the Lord Protector of Math.

Today I'm going to be reviewing limits.

Our Calculus book defines limits like this:

"We write
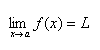and say 'the limit of f(x), as x approaches a, equals L'

if we can make the values of f(x) arbitrarily close to L by taking x to be sufficiently close to a but not equal to a."

So, to put this a little less pretentiously,
L is the value that f(x) is approaching as x approaches a.

One of the main things to remember when dealing with limits is:

LIMITS ARE TRENDS.

Still having trouble remembering? Maybe this creepy comic book guy will help you remember.



It is also helpful to ask yourself this question:
What value is y approaching as x approaches the limit?

There are two main ways that we have learned to estimate the value of limits.

The first method is numerically.
With this method, we plug in values that are close to the limit, and see if we can spot a trend.

The second method with which we can solve limits is algebraically.
To use this method, we plug the value that x is approaching into the equation.
Look at this picture:


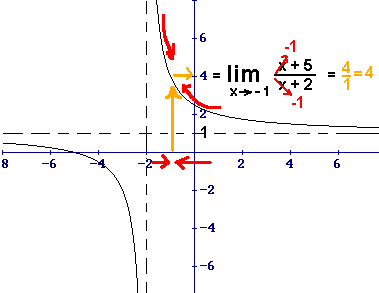We can see here that this equation has been solved algebraically, and a graph has been drawn to make the concept a bit clearer.

With the graph, we can see that as x approaches -1, y is approaching 4. When -1 is plugged into the equation for x, 4 is the number we obtain.

And remember, even when plugging in values gives you undefined, the equation can still be solved! If you want to solve it algebraically, try factoring. Or, you could always try to spot the numeric trend.

Try this example problem:

Guess the value of.

Now, the equation is not defined when x = 1, but it doesn't matter because the concept of a limit tells us that we are considering values close to 1 but not equal to it.

Let's try plugging some values into the equation.
x = 0.5, f(x) = .6666666667
x = 0.9, f(x) = .526316
x = 0.99, f(x) = .502513
x = 0.999, f(x) = .500250

Are we noticing a trend here?
We can safely guess that = 0.5

Here's a link if you want further clarification of the concept:
http://www.coolmath.com/limit1.htm

Reminder: Kate, it's your turn tomorrow!

See you all tomorrow!