3.8 Derivatives of Logarithmic Functions

Hi, guys. So right now, we're just finding a bunch of ways in which we can make finding derivatives easier. This section, we find out how to find derivatives of logarithmic functions. The lesson itself is pretty short. If you do the derivative of:



you get:



From this, we can generate the general theorem that:



In verbal terms this means that the derivative of the function ln of x equals one divided by x
Don't forget, however, that the chain rule still applies. So if you have this problem for example:



The answer is:



Notice how we first just differentiated the ln of x squared as a whole. Then we differentiated what was inside the parentheses--the x squared itself.

These are very helpful rules because they help us solve many problems that otherwise we wouldn't know how to solve! Like this one!

Find the deriviative of:



How do we do that? With the natural log derivative theorem of course! There are several steps to applying this rule to a problem. These steps are also a general rule of thumb that you can use with any logarithmic equation.

1) Take the natural log of both sides
So:



All we did was take the natural log of both sides

2) Simplify with the help of logarithm laws.
Don't forget from last year that there are several other rules about derivatives that we can use to help us. First off, remember that:



Oh look! We just happen to have the log of a quotient! Perfect!

So this means that our new result is:



The other logarithm rule we should remember is:

This helps us to since we have a a logarithm of a product. So now we have:



Now don't forget the rule where you can take the exponent of a logarithmic function and put it in front of the logarithm. Like this:



So since each of our three terms have exponents, we can just put those exponents in front of each term like so:



3) Use implicit differentiation for x

We know that:




So now we can apply this to our problem. Remember, don't forget to use the chain rule to those that have more than just x inside the ln ( ).



See where we had to use the chain rule? The 2x is the derivative of the x squared plus one and the 3 is the derivative of 3x + 2.
Notice also that we had to differentiate the y also. We had to use chain rule for that too, since 1 over y is the first term, and then we're still left with the y, which we had to differentiate by itself, giving us y prime.

4) Solve for y prime



Oh, but what does y equal? We know from the original equation. So we can go ahead and substitute that in, giving us our final equation:



Yayyy! We did it!
Here's something cool, guys. It's a very simply step-by-step proof of how they "derived" the formula for finding derivatives of logarithmic functions. Enjoy!
http://ltcconline.net/greenl/courses/116/ExpLog/logDerivative.htm

I thought these comics were funny. Mr. French, I couldn't remember if you had the amazing plusman on your wall or not. So I put it up anyway.







You're next, Laurie. And then the cycle starts all over!

Friday's Quiz Topics

First, I goofed – the last “5” on the TWS should be problem #59…

Here’s a list of topics that will be covered on this Friday’s Quiz. I’ve included the relevant homework problems…

Quiz – Sections 3.4-7
Derivatives of Trigonometric Functions (Sec. 3.4, # 5,7,29)
Chain Rule (Sec. 3.5, #13,53)
Implicit Differentiation (Sec. 3.6, #7,17)
Higher Order Derivatives (Sec. 3.7, #39)
Position/Velocity/Acceleration/Speed (Sec. 3.7, #49)

Remember that these topics can be mixed and matched, along with applications of the Product and Quotient rules!
I’ll be in early tomorrow and Friday. After school on Thursday, I have to leave at 3:00. See you in class!

"I believe in looking reality straight in the eye and denying it."
- Garrison Keillor (1942-) US author, producer

And remember, speed is relative:

3.7 Higher Differentiation

There were three main concepts in this section:

There were three main concepts in this section:
1. learning how to take second, third, fourth (etc) derivatives
2. New Notation for Higher Differentiation (dy/dx)
3. Relating the 2nd derivatives to motion and acceleration

Second, Third and Fourth Derivatives

Example:

Higher Derivatives:












Using dy/dx notation
Example:














Another Example:
y = sin (x)
y ′ = cos (x)
y ′′ = -sin (x)
y ′′′ = -cos (x)
y(4) = sin (x)
y(121) = cos (x)

The Second Derivative explains how the slope is changing. It tells us whether the graph is getting steeper or flattening out. In motion, the second derivative is used to measure acceleration.
s′ = v - the derivative of the distance equation is the velocity
v′ = a - the derivative of the velocity equation is the acceleration
s′′ = a - the second derivative of the distance equation is also the acceleration

Motion Example:
Initial Velocity--after one second-- Final Velocity--------- acceleration
10 mph------------------------------------ 20 mph--------------- +10 mph/sec
10 mph------------------------------------ 0 mph----------------- (-10) mph/sec
-10 mph---------------------------------- (-20) mph------------- (-10) mph/sec

Speed vs. Velocity
Speed = the magnitude of the velocity vector. It lacks direction.

When the change in velocity and the acceleration have the same sign (positive or negative), then the speed is increasing

Example:
Find the velocity and acceleration equation:



Find when the particle is speeding up:
-First find when the particle is at rest.
v = 3(t – 1)(t – 3)
-the velocity is equal to zero at 1 second and then at 3 seconds
-Then, test the intervals of velocity
- between 0 and 1: positive
- between 1 and 3: negative
- greater than 3: positive
-Finally, find when the acceleration is going to be 0
- a = 0 at 2 seconds
- Compute when acceleration is going to be positive or negative
- below 2 seconds: negative
- greater than 2 seconds: positive
-When the signs match, the particle is speeding up
So: 1 < t < 2 and t > 3

Here is a link for more information:
http://www.intmath.com/Diff/9_HiDe.php


SO there's the end of the blog for today folks.
-Lauren

Here's something to make you all very happy that it's Thursday:


DOESN'T IT MAKE YOU FEEL ALL WARM AND FUZZY INSIDE??


JAMES, have fun with the next one.

3.5 The Chain Rule

Sorry Mr. French....it said my html code was wrong so I had to start from scratch. Fingers crossed that this works!

Hello Section B.

Just as I like changing colors on Mr. French's interactive whiteboard, I also like changing blog colors...quite innovative don't you think?

If this goes anything like the chain rule homework, I will spend plenty of time doing unnecessary things only to realize that the solution to the problem is much simpler than I thought, redoing the hour and a half of work (which so far is like 3 and a half for the blog cuz it is having some compatibility issues) in about ten minutes.

ok, let's dive in:

The Chain Rule: Deals with composite functions. A composite function is a function within a function. There are 3 steps to follow when using the chain rule:

Step 1: Take the derivative of the inside function.
Step2: Take the derivative of the outside function by finding the value of the inside function with respect to x (do NOT, I repeat, do NOT take the derivative of the inside function in this step).
Step 3: Multiply Step 1 and Step 2.

Now let's put all that English into Mathematical Notation:

F(g(x))
F'(g(x)) = F'(g(x))g'(x)
I always like to write out these two lines because I find it keeps the problem in order and ensures I will remember the whole chain rule and fully apply it.


Example:
F'(6) = 7
g(3) = 6
g'(3) = 4
Step 1:
g'(3) = 4
Step 2:
g(3) = 6
F'(g(3)) = F'(6) = 7
Step 3:
4x7 = 28

Another way to apply the chain rule:
Fill in u for the inside of the function (this helps so that you don't forget steps because the u's should all be gone by the end of the problem):

Example:
F(x) = (3(x^2)+4x)^2 = (u)^2
F'(x) = (2u)(6x+4)
(The derivative of the outer)x(the inner as is)x(the derivative of the inner)
Plug in the inner function for the value of u:
F'(x) = 2(3(x^2)+4x)(6x+4)
F'(x) = 2(18(x^3)+36(x^2)+16x)
F'(x) = 36(x^3)+72(x^2)+32x

You can also foil the equation if you forget how to apply the chain rule on a test, but when the exponent is larger than w, it is an inefficient use of time.

The Power Rule Combined with the Chain Rule:
d/dx (u^n) = n(u^(n-1))x(u')

Example:
F(x) = (6(x^3))+2(x^2))(^100)
Step 1: Multiply the coefficient by the exponent from F(x):
F'(x) = 100(6(x^3)+2(x^2))
Step 2: Subtract 1 from the exponent of F(x) and insert the new exponent (this uses the power rule):
F'(x) = 100(6(x^3)+2(x^2))(^99)
Step 3: Multiply the whole quantity by the derivative of the inside function:
F'(x) = 100(6(x^3)+2(x^2))(^99)x(18(x^2)+4x)

Derivative of an Exponential Function:
d/dx (a^x) = (a^x)(ln a)
The derivative of an exponential function = (the function)x(the natural log of the base)

Example 1:
F(x) = (2^x)
F'(x) = (2^x)x(ln 2)

Example 2:
F(x) = (e^x)
F'(x) = (e^x)x(ln e) = (e^x)x1 = (e^x)

One more thing that is not new, but is a helpful reminder:
F(F'(x)) = x
(e^ln x) = x

If you need a little extra help, here is a good website to visit. It has really good examples and provides a full explanation of the chain rule. The home of the website has many more math resources, but this is the link to the chain rule page only (the link is not yet active...you will just have to wait until tomorrow morning):
http://www.math.hmc.edu/calculus/tutorials/chainrule/

As much as I adored posting my blog, I guess I will relinquish the duties of 3.6 to you ZAK.

Quote of the day:
"Yesterday is history,
Tomorrow is a mystery,
Today is a gift,
That's why we call it
The Present."

3.6 Implicit Differentiation

So far this chapter we have dealt with functions that express one variable in terms of the other. Or in other words, fuctions that explicitly defined. For example:

or

But now we must learn to deal with functions that do not express one variable in terms of the other, aka implicit functions. For example the fuctions:

are implicit functions because y is not described in terms of x.

So what does this mean? It means that we have a whole new way of finding the derivative of y without needing to solve for an equation for y in terms of x. Instead we now can use the method of Implicit Differentiation.

The method of implicit differentiation involves differentiating both sides of the equation with respect to x and then solving the equation that's left for y'.

For example let's take the equation:

and find the derivative.

1) First we must find the derivative of y squared

We already know that


So therefore by the Chain Rule


2) Now we must differentiate the entire equation

Here we must use the power rule, the product rule, and the known derivative of y squared to solve

3) Now we must solve for y'



factor out the y'


and that's our answer. Not too bad I'd say. I hope this implicit differentiation sample problem will help you guys in the future. Lauren Vons, you're up next!

The following are just a bunch of funny signs that don't pertain to math at all. They're just stupid so I thought you guys might like 'em.

3.4 Derivatives of Trigonometric Functions

Hey guys. Let's expand our growing knowldge about derivatives, shall we?

So basically, 3.4, the class favorite, is about finding the derivatives of trigonometric functions (you know...like sine, cosine, tangent...all that fun stuff).To start off, let's use y=sin(x) and find the derivative by graphing.

f(x)=sin(x):


And now...after marking the zeros and the slopes at the right points...f(x)=sin(x) and its derivative (in red):
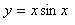
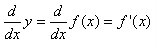
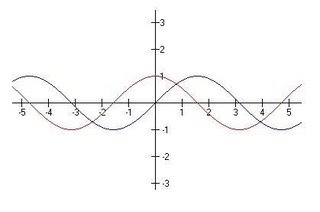
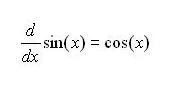Wow..doesn't the derivative of the sin(x) graph look oddly like the graph of f(x)=cos(x)?? Well it is! So thus:Now, let's do the same thing to the f(x)=cos(x) graph in order to find the its derivative.

f(x)=cos(x): After making the derivative graph (in red), you get this: Incredible. It looks to me that the derivative of the cosine graph is:
Knowing the derivatives of sine and cosine, the you can find the derivative of tangent. How? look below.
The derivatives for the inverse trig functions are as followed:
Sample Problem as follows: Okay SOPHIE you are up next!