3.6 Implicit Differentiation

So far this chapter we have dealt with functions that express one variable in terms of the other. Or in other words, fuctions that explicitly defined. For example:

or

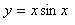
But now we must learn to deal with functions that do not express one variable in terms of the other, aka implicit functions. For example the fuctions:

are implicit functions because y is not described in terms of x.

So what does this mean? It means that we have a whole new way of finding the derivative of y without needing to solve for an equation for y in terms of x. Instead we now can use the method of Implicit Differentiation.

The method of implicit differentiation involves differentiating both sides of the equation with respect to x and then solving the equation that's left for y'.

For example let's take the equation:

and find the derivative.

1) First we must find the derivative of y squared

We already know that


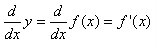
So therefore by the Chain Rule


2) Now we must differentiate the entire equation

Here we must use the power rule, the product rule, and the known derivative of y squared to solve

3) Now we must solve for y'



factor out the y'


and that's our answer. Not too bad I'd say. I hope this implicit differentiation sample problem will help you guys in the future. Lauren Vons, you're up next!

The following are just a bunch of funny signs that don't pertain to math at all. They're just stupid so I thought you guys might like 'em.