2.9: The Derivative As A Function

Hi guys! I hope you're having a good 3-day weekend.

One of the main points for lesson 2.9 was to replace a in the equation:



by the variable x. The new equation will look like this:



This new equation will work for all general situations involving x as a variable, and will allow us to find the slope of a tangent line/derivative/instantaneous speed at any point.

We also learned to draw the derivative just by looking at a graph:

1. Figure out where the zero's are (at the maximum and minimum points of the 'humps' of the graph-where the slope of the tangent line is 0). For example, if one of the maximum points on the graph was (2,7)- you would plot a point at (2,0).

2. Pick a few points on the graph and estimate what the slope of the tangent line to those points will be. Lets say you pick the point (5,10). If the slope of the tangent line to that point is around 6, you'll plot the point (5,6).

3. Connect all the points you've plotted, and you'll get a graph of the derivative!!

This website is really a helpful way to practice graphing derivatives:

http://www.math.uri.edu/~bkaskosz/flashmo/derplot/

So check it out!!!

There are other shorthands for derivatives that are also known as "differentiation operators," because they indicate the differentiation- also known as the process of calculating a derivative. They are as follows:



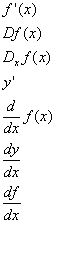
PS: Mr. French said that his favorite shorthand is dy/dx!

Now how do you know if a function is differentiable?

Well, a function f is differentiable at a if f'(a) exists. It is differentiable on an open interval (a,b) [or (a, infinity) or (-infinity, a) or (-infinity, infinity)] if it is differentiable at every number in the interval.

That was the book definition. In more simple terms, a function is differentiable if you can take a derivative or draw a tangent line to it. Differentiablity implies continuity, and f(x) is continuous over an interval or over a point if it is differentiable.

There are a couple continuous exceptions that are not differentiable at certain points. Let's take a look:





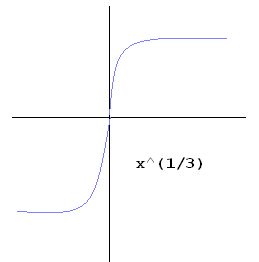
The equation of x^1/3 is not differentiable at x=0. It is a continuous function with a spot of discontinuity. The tangent line is vertical so the slope is undefined, and it is not differentiable at that point.




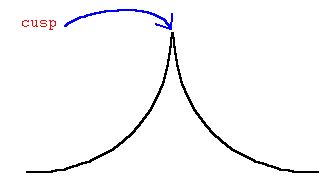
That graph has a cusp, so you can't draw a tangent line- the derivative is undefined so the function is not differentiable at the point of the cusp.

Also, if you have a graph of a jump discontinuity, the point where the graph "jumps" has no definitive slope, and is discontinuous and undifferentiable at that point.

Sample Problem



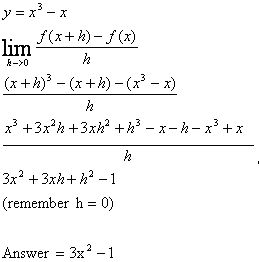
This website is also really helpful if you're having trouble with derivatives: (somehow it wont show up if i put it in link form... so just take out the astericks (*) and past it into your browser. http:**//people.hofstra.edu/faculty/stefan_waner/realworld/tutorials/frames2_4.**html

-Gianna you're next!