Section 2.6: Inifinite Limits and Horizontal Asymptotes

In this chapter we study big numbers. Really big. Or, as the book puts it, “arbitrarily large.” The question of this chapter is, what happens to the limits of functions as their x values reach infinity (also called the end behavior)? The answer lies in The Great Battle between numerators and denominators, top and bottom, big and small.

Basically, the two combatants in this Great Battle are the top variable in the function and the bottom variable in the fraction. Once you’re dealing with infinity, you can disregard the adding and subtracting portions of the functions. They’re arbitrary. There are three circumstances by which this Battle can be ended:

1. The bottom wins – this means that, as the x value reaches infinity, the bottom variable becomes the far greater of the two (most likely because it has a greater degree than the top x value), which brings the limit as x approaches infinity closer and closer to zero. Thus, the limit when the bottom wins is 0. For example:
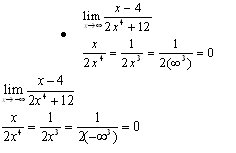
2. The top wins – here, as the x value reaches infinity, the top grows extremely large, getting closer and closer to...INFINITY! Hence, when the top wins the battle for greater degree, the limit becomes positive or negative infinity. Thus, the limit when the top wins is infinity. For example:
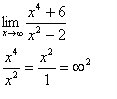
3. They tie – in this case, when the degrees of both leading variables are the same, Battle goes to the leading coefficients of these variables. For example, here the horizontal asymptote is 3/2:

One thing to watch out for—Radicals! Never forget that numbers under the radical sign always need to be positive. So, with that in mind, a few examples: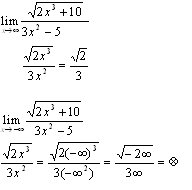

• Remember, you can't take the square root of a negative number. Dang. Gotta watch out for that one.

Yay, sample problem time! Now you get a chance to put your newfound skills to work!

Find the limit of: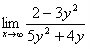

Work:

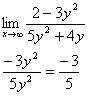
That wasn't so hard, now was it? No, I didn't think so. Well, if you need more help, here's a site.

Your turn next, Mark. Have fun!

n!