3.3 Rates of Change in the Natural And Social Sciences
Hey Guys! So this is that time of the year when we ask why on earth are we learning Calculus and how it applies to the "real world". Well, lesson 3.3 tells it all. Oh and I hope you guys don't mind that I'm using a purplish blue font. I thought it would spice things up a bit.
Like Laurie said in her wonderful blog posting of 2.8, "the slope of the tangent line = instantaneous rate of change = derivative." In science, the instantaneous rate of change is basically a change in position. An example in biology could be the diffusion of blood into a cell. In physics, the change in position is the measure of velocity (which is measured in acceleration). Let's focus on physics.
The position equation is usually given in the problem. Then from the equation, we are asked to find the velocity equation, the speed at a given time, time when we are at rest, time when we are moving to a certain direction, and the total distance traveled in a given time.
Now let's take a look at an example because words can be confusing...
The position equation of a particle is:
The questions are:
1) What's the velocity equation? (this means the DERIVATIVE...oh yes)
So we proceed to find the derivative using our handy power rule:
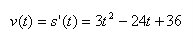
2) How fast is the particle moving at 3 seconds? (pluh and chug time)
Solution: The particle is moving to the left at 9 ft/sec
3) When is the particle at rest?
Soltution: At 2 sec and 6 sec.
4) When is the particle moving to the right? ("right" means it has a positive velocity)
On a number line, it looks like this: ![]()
5) What's the total distance traveled in the first 8 seconds?
This problem is a wee bit more complicated because we have to calculate four values. We look at the intervals that are consistent in the distance. First, we need to calculate the distance from t= 0 to t= 2. Then we need to calculate the distance from t= 0 to t=6. Finally, calculate the distance from t= 2 to t=6.
The best and easiest way to solve this problem is to use our calculators. (thank goodness)
- Type the equation into the y1 of the graphing screen
- In the normal screen, type y1 (0), y1 (2), y1 (6), y1 (8) (these are all the intervals)
Between y1(0) and y1(2) is 32ft forward. Between y1(2) and y1(6) is 32 ft forwards. Between y1(6) and y1(8) is 32 ft forwards. After we add the answers together, we get 96 ft as our total distance.
Solution: 96 feet
The site I found isn't a site you can practice problems on because this is more of an application problem. But, it does explain the concept pretty well. Once you reach the site and have read the info, go into more detail by clicking on the linked blue words. For example, click velocity on the "differentiable equations" page. http://hyperphysics.phy-astr.gsu.edu/hbase/diff.html
Now, remember on the first day of school (the good old days) we talked on this blog about math and religion? Well this is what it means to me:
alison noritake. i believe you are the next scribe for 3.4! Have fun!!!

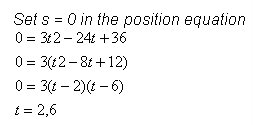
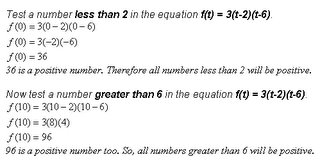

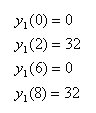


1 Comments:
oh sorry....i realized a second after i posted that the font is kinda small. sorry!!!
Post a Comment
<< Home