Chapter 3 Test: #16

A particle moves along the x-axis, its position at time t given by where t is measured in seconds and x in meters.

To find when the particle is speeding up, you first have to find both the velocity and the accelleration equations.

To find the velocity equation, you take the first derivative of which is because of the power rule.

To find the accelleration equation, you take the second derivative of 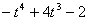which is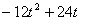

Then, you have to find the zero's for each equation. What I did was plug it into my Quadratic equation solver in my calculator. So, do that and you'll find that the zeros for are 0 and 3, and the zeros for are 0 and 2.

Now, you have to figure out whether you get positive or negative values between each zero. So, I drew two lines like this:


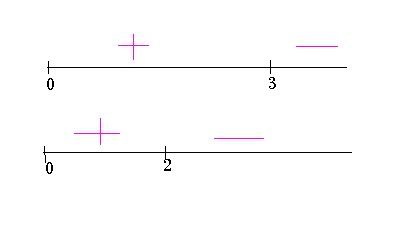
(Pretend that there is a line connecting 0 and 3.... I dont know what happened to it)

Where did those positive and negative signs come from? Look:

Just focus on the velocity equation, and plug in a number between its zeros (between 0 and 3) and you'll get a POSITIVE number. Now plug in a number that's greater than 3. You'll get a NEGATIVE number.

Look at the accelleration equation now. Plug in a number between its zeros (0 and 2) and you'll see that its POSITIVE. Plug in a number greater than two, and it's NEGATIVE.

The particle is speeding up when BOTH accelleration and velocity is positive, or when both are negative. As you can see, both are positive between 0 and 2. And both are negative when a number is greater than 3. So, your answer is

2 > t > 0 or t > 3

I hope that helped!

PS- I found out a really easy way to upload equations/pictures onto here!!! You just press "add image" and then you can add one directly from your computer! You don't even need photobucket. I'm sure everyone else already knew this but I didn't, so yay it was an exciting realization for me.

-Tessa