3.11 Linear Approximations and differentials
 Linear Approximations
Linear ApproximationsAccording to the graph, f' (x) = dy / dx
dy = f' (x) dx, dy = f' (a) dx
y-y1 = f' (x) (x-x), y =y1 + f' (x) (x-x),
y = f(a) + f' (a) (x-a),
L(x) = f(a) + f' (a)(x-a) or Δy = f(a + Δx) – f(a)
It was very exciting in class to finnally see why it is dy / dx - the slope of the tangent line.
This tangent line approximation or linear approximation of a at b is also referred to as linearization.
Differentials
Linear approximations are often formulated via differentials.
Let y = f(x) be a differentiable function.
The differential of x, dx, is an independent variable.
The differential of y is defined as
The differential of x, dx, is an independent variable.
The differential of y is defined as
Tangent line PR is, as we know, the derivative of f' (x). So, dy is the rise, the distance from S to R. We can see dy ≠ Δy. Δy is the amount that the curve rises when the x changes by the amount of dx.
Relative error is found by dividing the error by the total (ΔV / V). When multiplied by 100, we can find the percentage error.
Example
Find the value of y = √(25.001)
y = √(x + 25) .001 ≈ 0 so our a-value = 0
f(x) = √(x + 25)
f' (x) = (1/2) (x + 25)^(-1/2)
f(a) = √(0 + 25) = 5
f' (a) = (1/2) (0 + 25)^(-1/2) = 1/10 (*For these equations go to the f(x) and f' (x) equations found above and plug in x with a and the a-value. Do not find the derivative of f' (a) by differentiating the f(a)-value - that will just be zero.)
L(x) = 5 + (1/10)(.001-0)
L(x) = 5 + .0001 = 5.0001
√(25.001) ≈ 5.0001
Another type of problem you might see will ask for a prediction (probably extrapolating) after giving some data. With the data, we can plot a graph or make a table. When the question asks for the y-value after giving an x-value, the most accurate estimate will be found by finding the derivative of the closest given x-value. Then the y-value of the new x will approximately equal the y-value of our old x plus the derivative of the new x times the difference between the new and the old: f(x) ≈ f(a) + f' (a) (x - a) (which is the same as the definition for L(x))
Additional Internet Sources
Flash
Visual Calculus - Differentials
Visual Calculus - Linear Approximations
Powerpoint
Linear Approximations and Differentials
Reminder: Evan, it is your turn again... (but not until Monday, I believe)
Personalization
Although math puns are the first sine of madness, I do enjoy making them.
I am quoted in this article about Degrassi!
 Rocko knows to be hot, naughty, and courteous.
Rocko knows to be hot, naughty, and courteous.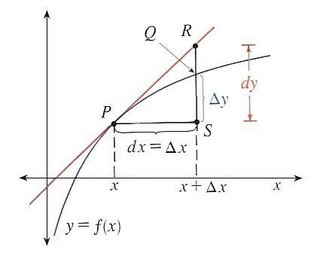

2 Comments:
I liked your example because you had to use exponents, which is what was throwing me off on the homework.
Your graph is also really useful in distinguishing how dy is not equal to change in y. The visual makes it much more comprehensive.
Rocko = A+
~8)
AHAHA! Jenny, the graph is brilliant. Not to mention colorful. But yes, it is quite helpful.
I think I've finally understood what the dx/dy notation means.
And yes, Rocko is mucho coolio. Foolio. =]
Post a Comment
<< Home