3.10: Related Rates

Hi everyone. This is Isabella, not Laurie; we traded places a while back, so I am officially our last scribe this first time around. Exciting.

Well, for the last few days, we’ve been battling with…RELATED RATES. These are all word problems, which have a tendency to be daunting. But if we break them down, they aren’t as monumentally frightening.

The key with related rate problems is to establish what information we’ve got and what information we are looking for. We also need to set up a static equation, which we will then differentiate to isolate our unknown.

So, before we look at some sample problems, let’s set up our rules:

1. Draw a picture. This helps you understand how the different components of the problem affect the overall situation.
2. Know what information is given and what information is unknown.
3. Set up a static equation, which presents the information when it is NOT CHANGING. The static equation defines the relationship between your variables.
4. Differentiate your static equation, which presents the information when it is changing with respect to time.

A very important thing to remember with differentiating is that we must still use our differentiation rules! Never forget about Product Rule, Quotient Rule, and particularly Chain Rule (that’s the one we always seem to mess up a tad). Precise differentiation is what gets us going when doing related rates problems.

All right, to make things clearer, let’s go to our examples.

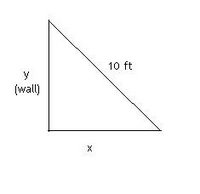
EXAMPLE 1: The Ladder Problem

A ladder 10 ft long rests against a vertical wall. If the bottom of the ladder slides away from the wall at a rate of 1 ft/s, how fast is the top of the ladder sliding down the wall when the bottom of the ladder is 6 ft from the wall?

Drawing a picture, we can see that the ladder, 10 feet long, is the hypotenuse of a triangle. The vertical wall is one leg, y feet long. The distance from the wall to the bottom of the ladder is the second leg, x feet long.

The information we are given is:

1. The length of the ladder (hypotenuse) = 10 ft

2. The distance (x) from the wall to the bottom of the ladder = 6 ft

3. The rate of the ladder sliding away from the wall = 1 ft/s

The word “rate” immediately tells us this will be a derivative. Since it is the rate of change of the horizontal component, x, this derivative is (dx/dt).

The information we are looking for is the rate of the ladder sliding down the wall—the rate of change of the vertical component, y, with respect to time, or (dy/dt).

Looking at the relationship between x and y, we can come up with our static equation:

x² + y² = 10² (A simple Pythagorean relationship)

Next, we differentiate EACH SIDE of the static equation (with respect to t = time).

2x (dx/dt) + 2y (dy/dt) = 0

Notice the use of the Chain Rule to differentiate x² and y².

Since we are looking for (dy/dt), we solve our equation for this unknown:

(dy/dt) = - (x/y)(dx/dt)

Now, we can substitute in our given information to find the unknown. We are given x and (dx/dt). To find y, we can just plug x into our original Pythagorean equation.
6² + y² = 10²
y² = 64
y = 8

We now have all information except the unknown. Plugging everything in:

(dy/dt) = - (6/8)(1 ft/s) = -(3/4) ft/s

So, the top of the ladder is sliding down the wall at a rate of (3/4) ft/s. Remember that the negative merely indicates that the distance from the top of the ladder to the ground is decreasing.

Not too bad, right? These problems can get more complicated, but as long as you follow the same procedure and keep track of your information, you can figure it out.

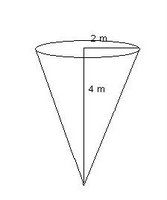
EXAMPLE 2: The Cone Problem

A water tank has the shape of an inverted circular cone with base radius 2 m and height 4 m. If water is being pumped into the tank at a rate of 2 m³/min, find the rate at which the water level is rising when the water is 3 m deep.

Sketching the cone, we see that the radius and the height are always legs of similar triangles.

Now, let’s identify our given information:

1. Radius (leg of triangle) = 2 m

2. Height of cone (leg of triangle) = 4 m

3. The depth of water (height in the cone) = 3 m

4. The rate of water being pumped into the tank is 2 m³/min.

Again, “rate” indicates a derivative. This time, it’s the derivative of the volume of the cone. Notice how “m³” hints that we’re dealing with a volume (just like “m²” would indicate area).

What’s our unknown? The rate at which the water level is rising. Since this is the rate of the vertical component, we know that is it the derivative of h with respect to time, or (dh/dt).

All right, now that we’ve got all that established, we can set up our equations.

Our static equation relates radius and height—the equation for the volume of a cone.

V = (1/3)(pi)r²h

It’s useful to work with V as a function of one variable, not two. Because we have more given information about h, we should eliminate r. Using the given information:

(r/h) = (2/4) so r = (h/2)

Now we can plug this into our static equation:

V = (1/3)(pi)(h/2)²h = (1/3)(pi)(h²/4)h = (pi/12)h³

Next we differentiate both sides with respect to t = time.

(dV/dt) = 3 (pi/12)h² (dh/dt) (CHAIN RULE)

(dV/dt) = (pi/4)h² (dh/dt)

Solving for (dh/dt), our unknown:

(dh/dt) = (4/(pi)h²) (dV/dt)

Now we can substitute the information we were given:

(dh/dt) = [4/(pi)(3)²](2) = (8/9(pi))

So, the water level in the cone is rising at a rate of (8/9(pi)) m/min.

Let’s not forget that our variables can also involve angles and trig functions!

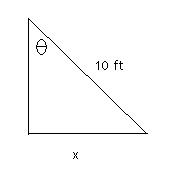
EXAMPLE 3: The Theta Problem

A ladder 10 ft long rests against a vertical wall. If the bottom of the ladder slides away from the wall at a speed of 2 ft/s, how fast is the angle between the top of the ladder and the wall changing when the angle is pi/4 radians?

Drawing the triangle, we see that the vertical wall is one leg of the triangle and that the 10-ft ladder is the hypotenuse of the triangle.

What information are we given?

1. The hypotenuse of the triangle = 10 ft.

2. The rate at which the bottom of the ladder is sliding away from the wall = 2 ft/s. This is the derivative of the horizontal component, x, of our triangle, or (dx/dt).

3. The angle between the wall and the ladder = pi/4 rad.

And our unknown? The rate at which the angle between the ladder and the wall is changing. This is the derivative of the angle, or (d(theta)/dt).

Looking at the triangle, we see that we can set up a relationship between the angle tbeta and one of the legs and the hypotenuse of the triangle. Because we know that x is the leg opposite theta, and we have a value for the hypotenuse, we can use sine to describe the relationship.

sin (theta) = (x/10) (opposite leg over hypotenuse)

This is our static equation. Differentiating, we have:

cos (theta)(d(theta)/dt) = (1/10) (dx/dt)

Remember that differentiating sin(theta) involves the Chain Rule, and that (x/10) is another way of saying (1/10)x—that is, (1/10) is the coefficient of x.

Now that we have our equation, we can plug in our information:

cos (pi/4) (d(theta)/dt) = (1/10)(2)

((rad2)/2) (d(theta)/dt) = (2/10)

We want to isolate (d(theta)/dt):

(d(theta)/dt) = (4/10)/(rad2) = 2 / (5rad2) = (2rad2)/10 = (rad2)/5

So, the rate at which the angle between the wall and the top of the ladder is changing is (rad2)/5 radians/sec.

Voila. Tricky, but not impossible. Related rates may seem scary, but as long as you organize (and don't panic), Related Rates will smile on you and perhaps befriend you. And we all know that everyone needs a friend, even one that tends to be fickle.

Here's a website that provides its own version of a procedure for a related rates problem. It also has two useful problems, including an example of a cone problem:
http://www.mathematicshelpcentral.com/lecture_notes/calculus_1_folder/related_rates.htm

I don't know how many of you know this bit of trivia, but...I am very fond of frogs. I think they're awesome. So, I thought I'd share with you guys a froggy image that is close to my heart.

Just barely hanging on...we've all had those moments.

We're back to the beginning of our scribe list, so Jenny, it's your turn tomorrow. Have a good night, everyone! ~8)