Chapter 3 Test #6

A table of values for f, g, f', and g' is given. If h(x)=f(g(x)), find h'(1).
x...f(x)...g(x)...f'(x)..g'(x)
1....-5.....3.......-2......-3
2.....4......2........1.....-10
3....10.....6........9......-9

so, since you are trying to find the derivative of h'(1), the general equation for the h'(x) is:


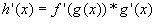
then, plug in 1 for x to get:


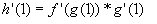
next, look at the chart above to find g(1), g'(1), and f'(whatever g(1) equals). you get:


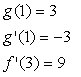
knowing these values, plug in those values for g(1), g'(1), and f'(whatever g(1) equals) respectively:


thus...h'(1) = -27

and theree you go.