Chapter 4, Lesson 2

I have honestly pondered this for years...since the first time I read it...

Ready for Round Two with Tooch?

So we went over two new theorems: The Mean Value Theorem ("mean" as in average, not "mean" as in not nice), and Rolle's Theorem. Let's review Rolle's theorem first, shall we?

Rolle's Theorem has three conditions:
Firstly, the function f must be continuous on the closed interval [a, b].
Secondly, the function f must be differentiable on the open interval (a,b)-->remember, a differentiable function means that every point is approachable from both sides, so this part must be an open interval
Thirdly and Lastly, f(a) = f (b) (This part is pretty definitive for the theorem)

If all these conditions are found to be true, then there exists at least one value c where f'(c) = 0

So, can we all see how that works? I can't get the picture to upload right now, but I plan on conferring with Mr French to fix that by Tuesday...

But think about it: if the end points of your graph have the same y-value, and the graph is continuous and differentiable, wouldn't there have to be a point where the slope is zero, because it has to return to the origianl y-value at some point.

All together now: Ooooooh, yeah...

So how would this theorem break down?
1.) If it is discontinuous (removable, asymptotic, or jump discontinuity).
2.) If it is differentiable (there is a cusp or kink). On a completely unrelated note, we missed you in class today, James. Hope you're enjoying St. Louis!
3.)

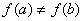
Let's look at this last one a bit. Suppose the y-values for a and b were different. Then what? If we look at the first theory, we can figure out that the line segment connecting a and b is 0, the same as the derivative at point c. So they are parallel, yes? (Do we remember Geometry? We have all three of the Geometry Senior Leaders in our section, so you should!) Anywho, if the endpoints' y-values are different, there's still a line connecting them, yes? Would it not be logical to assume that there is at least one point with a tangent line parallel to this new line?

My friends, welcome to the Mean Value Theorem.

If function f is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), then there exists at least one value c such that



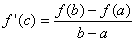
In other words, the slope of f'(c) is equal to the secant line between a and b.

I found this website that re-explains everything and provides sample problems to test your wit. Give it a shot if you're still confused.

Excellent...let's put it to use!

Here is a COMPLETELY ORIGINAL (not to brag or anything) sample problem, complete with solution.

I'm going to go through it in words, and then I'll give you the numbers. How do you like them apples?

We have f(x) = 2x^4 + 3x on the closed interval [0, 2]. How can we find (c, f(c)), the point where the tangent line is parallel to the secant line?

Let's start by plugging in both endpoint values We find that f(0) = 0 and f(2) = 38. From here, we do two things. Firstly, we find the derivative of x, using all of our miraculous rules and such. Then, we find the slope of the tangent line at point c, which we know is equal to that of the secant line through a and b. We then set the two equations equal to each other and solve for x, which will give us the x-value for c. We can then plug c back into our original equation to solve for y. Yay!

And our final answer: (1.259, 8.819) Yeah, I know, it's not very pretty, but deal with it. Did you make up the question?

One last thing before I go. Here's another way to conceptualize it. We have an unknown function, but we know that f(0) = 2, and that f'(x) is greater than or equal to 3 for all values of x. What is the smallest value possible for f(5)?

Here's the guidelines: You have the values for a, b, and f(a). Set f'(c) equal to 5 and solve for f(b).

I challenge you to solve it, and the first person who posts back the correct answer will get a small prize and tons of bragging rights (No, Mr French, you can't win, but I will be checking my answer with you.)

Taylor, you're up next! Have a good weekend, and everybody come to PrepStock!