4.1: Maximum and Minimum Values

I, the Lord Protector of Math, have returned. Unfortunately, my beast of a custom-built computer has died and I am reduced to working on this Mac. I don't have as much technical ability with Macs, so bear with me.

Well, thankfully for you guys, this section is pretty straightforward.

Let's start with a definition.

A function f has an absolute maximum (or global maximum) at c if f(c) is greater than or equal to f(x) for all x in the domain of f. The number f(c) is called the maximum value of f on D. Similarly, f has an absolute minimum at c if f(c) is less than or equal to f(x) for all x in D and the number f(c) is called the minimum value of f on D. The maximum and minimum values of f are called the extreme values of f.

Whew, that's quite a mouthful. Let me try to break this down.

An absolute maximum (also called the global maximum) would be the highest point on a graph in its domain. The number f(c) is called the maximum value of f on its domain.

An absolute minimum (also called the global minimum) would be the lowest point on a graph in its domain. This number f(c) is called the minimum value of f on its domain.

The maximum and minimum values are collectively known as the extreme values of f.

Pretty straightforward, wouldn't you say?

Let's get a diagram going.



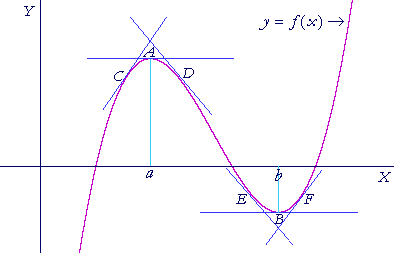
Hey, look, a diagram!
Here we can see that a and b are local maximum and minimum, respectively, for this function. This diagram also leads me to our next theorem, named:

FERMAT'S THEOREM

This theorem states that if a graph has a local maximum and mininum and it is possible to take a derivative, that derivative equals 0. You can see that illustrated in the diagram, where the tangent lines are drawn at the local max and min.

So, let's define local max and min:

A function f has a local maximum (or relative maximum) at c if f(c) is greater than or equal to f(x) when x is near c. Similarly, f has a local minimum at c if f(c) is less than or equal to f(x) when x is near c.

More technobabble. Let's define this more simply.
If a point is higher or lower than its immediate surroundings, such as in the above diagram, then it can be defined as a local maximum or minimum.

Just a little bit more. Stay with me, guys.

CRITICAL POINTS
I could make a bad pun and say I'm at a critical point with JPD coming and all that. But I'll spare you the agony and give you the mathematical definition.

A critical number of a function f is a number c in the domain of f such that either f'(c) = 0 or f'(c) does not exist.

To reiterate:

A critical point is when

1. f'(c) = 0
OR
2. f'(c) doesn't exist

Pretty simple.

Also,
If f has a local maximum or minimum at c, then c is a critical number of f.

ONE MORE THING!

The Extreme Value Theorem. So extreme, its inner workings can hardly be contained in this post.

If f is continuous on a closed interval [a,b], then f attains an absolute maximum value f(c) and an absolute minimum value f(d) at some numbers c and d in [a,b].

So, basically, if the function is:

1. Continuous
2. On a closed interval

Then there absolutely has to be an absolute maximum and minimum within that interval. Logical, right?

Want an example problem? Of course you do! (Unfortunately, due to the aforementioned dead computer, I don't have access to my photo editing programs. My bad.)



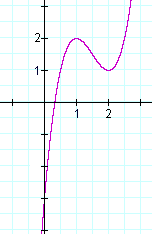
Try finding the absolute maximum and minimum, as well as the local maximums and minimums.

Abs max and min: Oops! Trick question! There is no absolute max or min, because the graph has an unlimited range.

Local max: There is a local maximum at (1,2)
Local min: There is a local minimum at (2,1)

Those are local because they are higher and lower, respectively, than the points around them.

Here's a cool link that explains this stuff pretty well.
Clicky clicky!

And remember, KATE, you're up next.

And, now, time for my obligatory picture from my archives of awesomeness.



Penguins are already great. Pirate penguins are just out of this world.

Well, I hope this post was as informative as it was long. I also hope you are not collapsed in front of your computer dying slowly of boredom.

Until next time, my children,

Evan, the Lord Protector of Math