5.4 Indefinite Integrals and The Net Change Theorem

Hey, it's Zak. I'm filling in for Sophie because she's all bogged down with other stuff. So she'll do 5.5 over break.

Anyway here's 5.4:

An Indefinate Integral is basically just like a definite integral except for the fact that it has no boundaries. A definite integral is limited by the values a and b whereas an indefinite integral is infinite, meaning the boundaries of a and b do not exist. Therefore, the notation for writing an indefinite integral is as follows:


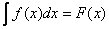
where

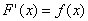
Notice how the notation does not have any values for a or b inputed above or below the integral sign. That's how an indefinate integral should be written.

Important: There is a big distinction between definite and indefinite integrals. A definite integral is a number whereas an indefinite integral is a function or family of functions. Also, since indefinite integrals are functions, the "+ C" cannot be disregarded when writing out the function. For example:

When finding the antiderivative of the function:

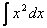
We get:

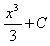
Whereas with boundaries, we'd get an exact number and not incorporate the "+ C"

Net Change Theorem: The integral of a rate of change is the net change. In other words, the value of the integral is an object's displacement from the starting point, not the total distance traveled. For example, if I walk 10 feet and come back 9 feet, my displacement is 1 foot but my total distance is 19 feet.

Sample Problem:
Given the equation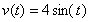find the displacement and total distance an object traveled in the interval

For this we can use our calculators:

Step 1: Enter the equation into Y1
Step 2: Go to the home screen and press (math) then (9) to get "fnInt" on the screen
Step 3: Enter 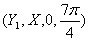after "fnInt"
Step 4: Press (Enter) and you should get an answer around 1.1715. This is your displacement.

To find the total distance:

Step 5: Go back to the equations screen and insert "abs" in front of the equation. This will prevent the graph from ever dipping below the x-axis, thus resulting in no negative distance and therefore representing the total distance and not the displacement.

Step 6: Follow steps 2, 3, and 4 again but this time you should get an answer around 14.828. This is the total distance traveled.

That's about it, hope that helped.

In the Humorous Spirit of the Holidays:
Mr. Church and Virginia may very well believe in Santa Claus, but some scientists have done some mathematical studies into the physics behind Santa Claus in order to prove that Santa Claus cannot physically exist. Needless to say, their results are very convincing (and humorous). So here they are:

A Scientific Inquiry into Santa Claus:

1) First of all, no known species of reindeer can fly. BUT there are 300,000 species of living organisms yet to be classified, and while most of these are insects and germs, this does not COMPLETELY rule out flying reindeer which only Santa has ever seen.

2) Secondly, there are 2 billion children (persons under 18) in the world. BUT since Santa doesn't appear to handle the Muslim, Hindu, Jewish, & Buddhist children, that reduces the workload to 15% of the total - which is 378 million according to Population Reference Bureau. So at an average (census) rate of 3.5 children per household, that's 91.8 million homes. And of course, one must presume that there's at least one good child in each.

3) Additionally, Santa has 31 hours of Christmas to work with due to the different time zones and the rotation of the earth, assuming he travels east to west (which seems logical). This works out to 822.6 visits/second which means that for each Christian household with good children, Santa has .001 second to park, hop out of the sleigh, jump down the chimney, deliver the presents, eat his milk and cookies, go back up the chimney, get back into the sleigh and move on to the next house. Assuming that each of these 91.8 million stops are evenly distributed around the earth (which, of course, we know to be false but for the purposes of our calculations we will accept), we are now talking about .78 miles/household, a total trip of 75.5 million miles. So Santa's sleigh must be moving at 650 miles/second, 3,000 times the speed of sound. For purposes of comparison, the fastest man-made vehicle on earth, the Ulysses space probe, moves at a poky 27.4 miles/second. A conventional reindeer can run, tops, 15 miles/hour.

4) Moreover, the payload on the sleigh adds another interesting element. Assuming that each child gets nothing more than a medium-sized lego set (2 lb.), the sleigh is carrying 321,300 tons, not counting Santa, who is invariably described as overweight. On land, conventional reindeer can pull no more than 300 lb. Even granting that "flying reindeer" (see #1) could pull 10 TIMES the normal amount, we cannot do the job with 8, or even 9 reindeer. Instead, we need 214,200. This therefore increases the payload - not counting the weight of the sleigh - to 353,430 tons which is four times the weight of the ocean-liner Queen Elizabeth.

5) 353,000 tons travelling at 650 miles/second creates enormous air resistance which will heat up the reindeer up in the same fashion as a spacecraft reentering the earth's atmosphere. Therefore the lead pair of reindeer will absorb 14.3 QUINTILLION joules of energy. Per second. Each. In short, they will burst into flame almost instantaneously, exposing the reindeer behind them thus vaporizing the entire reindeer team within .00426 of a second and all the while creating deafening sonic booms in their wake. Meanwhile, Santa will be subjected to centrifugal forces 17,500.06 times greater than gravity. Therefore, a slim 250-lb Santa would be pinned to the back of his sleigh by 4,315,015 lb. of force.

So if Santa ever DID deliver presents on Christmas Eve, there's no way he could've survived.

Sorry Virginia, sometimes facts are facts, but hopefully you never find out.

Sophie, you're up next, and you have all break to do it...