4.10: Antiderivatives

Hey guys!! So, I'm back to talk about the last section of Chapter 4: ANTIDERIVATIVES!! YAY! ok so let's go...

The book definition of an antiderivative:
A function F is called an antiderivative of f on interval I if


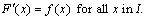
Now, let's take that definition and apply it to this next situation:

1.
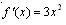if this is my derivative equation, what is the original f(x) equation?
YES!! it would be, its general form,



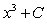
Now, you might be wanting to ask me, "Gianna, what does the antiderivative have to do with this? And, furthermore, what the heck does 'general form' mean?" To those questions, I would respond by saying that firstly, the antiderivate is the original f(x) equation so that answers your first question. As for the second one, an antiderivative's general form is, simply put, the generic one that contains the + C, which needs to become your new best friend by the way. Furthermore, the general form( general antiderivative) can be found easily. LOOK:







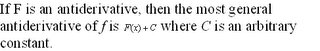
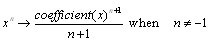
Now that we have this extra tool to help us, let's do some examples.















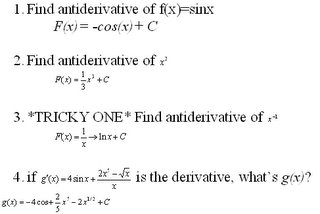
Ok, FANTASMIC!! Now that we are very comfortable with, or should be at least, the concept of the antiderivative, let's apply it to the real world questions about acceleration, velocity and position equations.




















Ok so now that we have a full knowledge of the antiderivative, we can call ourselves COMPLETE PEOPLE!! YAY!! So, Kristin, good luck and here's a comic to help you get going: