4.4 Indeterminate Forms and L'Hospital's Rule
Hey everyone. I guess I’m here to help you all learn about the wonders of section 4.4 – Indeterminate Forms and L’Hospital’s Rule.
The point of this lesson is to find out what’s going on near the ends of the graph at infinity.
Okay, I guess we’ll be doing an example problem to learn this lesson quickly.
Example Problem:
We’re going to solve this using L’Hospital’s Rule:
***L’Hospital’s Rule***
Suppose f and g are differentiable and
g’(x)≠ 0 near a (except possibly at a). Suppose that:
(In other words, we have an indeterminate form of type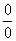
or
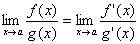
If the limit on the right side exists (or is infinite
Now, you always have to remember that the limit at infinity depends on how fast the top grows compared to how fast the bottom grows. And another thing to keep in mind, L’Hospital’s Rule can only be used when the limits are indeterminate.
There are 7 indeterminate forms of limits that we know of:
Although there are 7 indeterminate forms of limits, it’s usually best to try to change any the last 5 forms to one of the first two forms :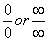
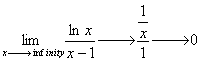
Now…you may be asking, “HOW do we do this?” It’s simple. First of all, we can see that if we had left the equation (ln x) / (x-1) alone and tried to find the limit by simply plugging “infinity” into ‘x’, the limit would become infinitely large. Eventually, “ln x” would become “infinity,” and “x-1” would also become “infinity.” Hopefully you realize that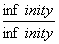
So using L’Hospital’s Rule, we rewrite the derivative of “ln x” as (1/x)(1) and the derivative of “x-1” as 1.
To find the derivative of this whole limit of a function, we don’t use the quotient rule. Instead, we take the derivative of the top (ln x) and divide it by the derivative of the bottom (x-1).
Eventually, we can find that the limit, as x approaches infinity, is zero.
To simplify the definition of L’Hospital’s Rule, here’s an equation to help you figure this thing out:
Well, I hope you understand all of this…but in case you don’t, we’ll try some different problems that use The Rule (sorry, I just don’t want to constantly type out L’Hospital’s Rule…which I just did…again. AHHHHHH!!!).
Using THE Rule, we find that the derivative of (3x2 + 4) is 6x, and the derivative of (2x2 + 7) is 4x. So we just put the top derivative over the bottom derivative, like this 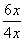
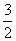 Another problem like this:
Another problem like this:
We used the Rule to find that the limit, as x approaches infinity, is 4! Huzzah!
Okay, last sample problem…this one’s a little different from the last two we’ve had.
Example:
Without using the Rule, we would find that the limit would be: 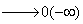
Now, don’t make this mistake. Although you might think that zero multiplied with negative infinity would equal zero, it doesn’t. Zero multiplied with negative infinity is actually an indeterminate form of limits. That means that we can use the RULE!
So we will re-do this whole thing using L’Hospital’s Rule:
First, let’s start off by showing that the limit becomes an indeterminate form of limits.
We can rewrite x so that it does not end up equaling zero.
Now that this is in an indeterminate form that we like, we use L’Hospital’s Rule:
Derivative of (ln x) divided by the derivative of (x-1) 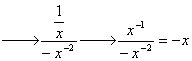
And no, Jean, this does not “become negative zero”…it is simply zero.
Hopefully you all understand this lesson now because I know I DO!
BUT, in case you still need help, you can go to these sites:
or


sorry about the blacked out equation...you can just click on it to see the equation...o, and sorry about this blue-underlined sentence...I don't know why it's doing this, but it's really annoying and I want it to stop...but it won't. So....I can't do anything.
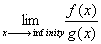
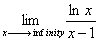
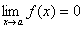
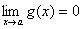

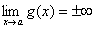
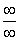
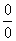

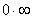
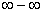

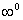
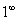
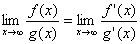


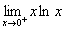
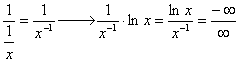

7 Comments:
sorry about the blacked out equation..you can just click on it to see the equation.
Oh, and I'm really hoping to be special like Sophie and get a comment from Mr. Jones from Scotland or from CP Throckmorton from Britain!!!!
wow, i'm really tired...so..i gotta go start my homework now. SO...byebye
John Cynn is a mean, mean boy who makes fun of girls who make stupid comments. Just wanted the world to know.
whoaaaa
the sentence "Just wanted the world to know." is...lacking a subject.
tsk tsk...seniors
Personally, I like the idea of negative zero - it opens up the possibility of positive zero, too! But is negative zero less than nothing? Hmmmm...
Mr French, you're making my head hurt with your deep mathematical thoughts...actually, I was thinking about that a lot yesterday too...
uhhh...i'm still waiting for Mr. Jones
Would Ms Farrell from Scotland do? I've met Mr Jones so I can tell you he's real!
I'm very impressed with all your equations. It's been a long time since I studied maths so I don't understand them, but they look very impressive ;-) Well done on a fantastic blog!
Post a Comment
<< Home