Chapter 3 Test, #10

Sorry I'm late, guys.

Anyway, the problem gives us the function



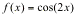
and asks us to find



In order to do this, let's first find the higher order derivatives of the function. Remember the chain rule!

The derivative of cos(2x) is:



Find the next derivative:



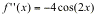
And the next:



Finally, it repeats itself, but with a higher coefficient.



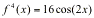
So, since it repeats at the fourth derivative, we divide the derivative we are looking for, 1428, by 4. And, conveniently, 4 goes into 1428 evenly. This means that we have to use the 4th derivative equation. If you will notice, with each derivative, the coefficent is two to the the power of the number of the derivative.

So, the equation is



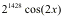
And there you have it!